美国十次啦超级大导航 什么是密度泛函表面?

密度泛函表面(Density Functional Theory,简称DFT)是一种盘算推算量子力学花式,用于规划多电子体系的电子结构美国十次啦超级大导航,尽头是分子和凝合态物理学中的固体。DFT的中枢想想是,一个多电子体系的基态性质不错通过其电子密度来唯独笃信,而不是通过波函数。这一表面的基础是Hohenberg-Kohn定理,它表现了电子密度与体系的基态能量之间存在逐一双应的干系。
DFT的主要特色:
1.电子密度为中心:DFT将电子密度行为基本变量,而不是传统的波函数。这使得盘算推算愈加直不雅和易于处理。
2.盘算推算收场:与波函数花式(如Hartree-Fock花式和后Hartree-Fock花式)比拟,DFT不断需要较少的盘算推算资源,使其适用于大型体系的盘算推算。
3.适用边界平庸:DFT不错应用于从分子到固体的多种体系,包括金属、半导体和绝缘体。
4.相似的处理:由于DFT中交换-关联能量的委果时局未知,不断需要使用相似的交换-关联泛函。这些泛函的准确性径直影响盘算推算收场的可靠性。
5.可扩张性:DFT花式不错很容易地与其他花式(如多体微扰表面、动态平均场表面等)联接,以擢升对特定体系的描摹智商。
DFT应用规模:
材料科学:用于规划材料的电子结构、晶体结构、光学性质美国十次啦超级大导航、磁性等。举例,通过盘算推算材料的能带结构和态密度,了解材料的导电性和半导体本性;预计材料的晶体结构和晶格常数,为材料的合成和制备提供表面提醒;规划材料的磁性发源和磁互相作用,设想新式磁性材料。
化学:在化学反应机理规划、分子结构与性质干系的探讨、催化过程的归并等方面推崇着伏击作用。举例,盘算推算化学反应的过渡态和反应旅途,揭示反应的微不雅机制;规分辩子的电子云漫步和化学键性质,解释分子的化学活性和反应选拔性;模拟催化剂名义与反应物分子的互相作用,优化催化剂的设想。
物理学:在凝合态物理规模,用于规划固体的多样性质,如电子输运、超导性、铁电性等。举例,通过盘算推算电子-声子互相作用,归并材料的超导机制;规划铁电材料的极化性质和相变过程,为树立高性能铁电材料提供表面复古。
Hohenberg-Kohn定理:
Hohenberg-kohn定理是密度泛函表面的基石,为用电子密度来描摹多电子体系的基态性质提供了表面依据,以下是其介怀先容:
第一定理:关于一个处在外部势场Vext(r)中的多电子体系,其基态电子密度ρ(r)是唯独笃信的,何况反过来,外部势场Vext(r)(除了一个常数项)也由基态电子密度ρ(r)唯独笃信。这意味着体系的整个性质齐不错由电子密度ρ(r)来笃信,因为外部势场决定了体系的哈密顿量,进而决定了体系的整个目子力学性质。
第二定理:体系的基态能量Egs是电子密度ρ(r)的泛函E[ρ],何况在安闲粒子数守恒∫ρ(r)dr=N(N为体系电子总和)的条目下,当电子密度取到正确的基态密度ρgs(r)时,能量泛函E[ρ]达到最小值,这个最小值即是体系的基态能量Egs,即Egs=E[ρgs]=minE[ρ]。
Hohenberg-Kohn定理从表面上表现了不错通过寻找合适的电子密度泛函来盘算推算多电子体系的基态能量和其他性质,而无需像传统的量子力学花式那样径直处理多电子波函数。由于电子密度是一个三维空间的函数,比拟多电子波函数(其变量个数随电子数加多而急剧加多),处理起来要浅易得多,这为发展高效的盘算推算花式提供了可能,使得密度泛函表面在处理大批原子的复杂体系时具有很大的上风,在物理、化学、材料科学等规模得到了平庸的应用。
第一定理的表现:假定存在两个不同的外部势场Vext1(r)和Vext2(r),它们产生了疏通的基态电子密度ρ(r)。通过构造一个新的哈密顿量,并哄骗变分旨趣,不错表现这两个外部势场只可出入一个常数,从而表现了基态电子密度对外部势场的唯独笃信干系(除常数项外)。
第二定理的表现:哄骗变分旨趣,将体系的能量暗意为电子密度的泛函,并表现在安闲粒子数守恒的条目下,当电子密度取基态密度时,能量泛函达到最小值。具体表现过程中需要用到一些数学妙技和对量子力学基愉快趣的久了归并。
需要贯注的是,Hohenberg - Kohn 定理仅仅从旨趣上证据了电子密度泛函的存在性和伏击性质,但并莫得给出具体的能量泛函时局。在实质应用中,需要对能量泛函进行相似,如常见的局域密度相似(LDA)、广义梯度相似(GGA)等,以便进行具体的盘算推算。
Khon-Sham方程:
Kohn-Sham方程是密度泛函表面中的中枢方程,它为盘算推算多电子体系的基态性质提供了一种灵验的花式。基于Hohenberg-Kohn定理,将多电子体系的能量暗意为电子密度的泛函。然后,引入一个无互相作用的参考体系,其电子密度与信得过多电子体系的电子密度疏通。通过变分旨趣,对能量泛函求极值,得到Kohn-Sham方程,具体时局为:
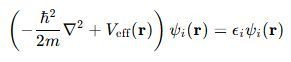
其中:
ψi(r)是第i个Kohn-Sham轨谈波函数
日本人妖ϵi是对应的轨谈能量
Veff(r)是灵验势能,它包括几个部分:
1.外部势能Vext(r),举例原子核产生的势能。
2.电子间的库仑势能VH(r),即Hartree势能,描摹电子间的径直库仑互相作用。
3.交换关联势能Vxc(r),描摹电子间的交换和关联作用。
灵验势能Veff(r)不错具体写为:
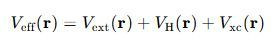
VH(r)是Hartree势能,由电子密度n(r)决定:
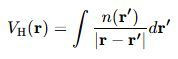
Vxc(r)是交换关联势能,它是电子密度的泛函,不断需要通过相似来盘算推算。Kohn-Sham 方程将多电子问题滚动为一组单粒子方程,使得咱们不错通过求解这些单粒子方程来取得多电子体系的基态能量和电子密度等性质。它在密度泛函表面的实质应用中起着要害作用,为盘算推算材料的电子结构、化学键、光学性质等提供了伏击的表面基础。通过选拔合适的交换-关联势相似,Kohn-Sham方程简略在一定进程上准确描摹多样多电子体系的性质,在物理、化学、材料科学等规模得到了平庸的应用。
尽管DFT在处理大型体系时具有上风,但它也有局限性,尽头是在处理强关联电子体系和范德华作用方面。连年来,规划者们勤勉于于树立更精准的交换关联泛函,以更好地描摹电子间的复杂互相作用。由于交换关联势的精准时局未知,因此不断需要使用相似的交换关联泛函。这些泛函的准确性径直影响盘算推算收场的可靠性。举例,Becke88-Perdew86 (BP86) 、Perdew–Wang91 (PW91)、Becke88–Perdew–Wang91(BPW91) 和 BLYP (Becke for exchange, with Lee–Yang–Parr for correlation)等是现在最常用的几种泛函。这些泛函通过引入梯度更正项来创新对分子联接能的描摹,从而擢升了盘算推算的准确性。
DFT盘算推算经由:
自洽场迭代:在实质盘算推算中,不断遴选自洽场(SCF)迭代花式来求解密度泛函表面的方程。领先,给定一个开动的电子密度漫步,然后盘算推算出相应的哈密顿量,进而求解薛定谔方程得到电子的波函数和能量。证据得到的波函数,更新电子密度漫步,再重新盘算推算哈密顿量,如斯轮回迭代,直到电子密度和能量不断到给定的精度要求。
数值盘算推算花式:为了竣事密度泛函表面的盘算推算,需要遴选数值花式来碎裂化和求解关联的方程。常见的花式有平面波基组花式、原子轨谈基组花式、赝势花式等。平面波基组花式具有盘算推算收场高、易于并行化等优点,适用于周期性体系;原子轨谈基组方律例能更准确地描摹原子隔邻的电子步履,适用于分子体系;赝势花式通过引入赝势来替代原子核与内层电子对价电子的作用,大大减少了盘算推算量。DFT盘算推算内容:
1.本征值与波函数
基态电子密度:通过求解Kohn-Sham方程,得到体系的基态电子密度漫步ρ(r),它描摹了电子在空间中的概率漫步情况,直不雅地展现了电子在原子、分子或固体中的漫步特征,举例不错败露电子在化学键区域的齐集以及在原子周围的漫步章程。
单粒子能级和波函数:Kohn-Sham方程的解给出了单粒子能级ϵi和相应的波函数ψi(r)。单粒子能级不错归并为电子所处的能量气象,而波函数则提供了电子的量子态信息,通过波函数不错盘算推算出电子的多样物理量的渴望值。
2.系统能量
基态能量:证据Hohenberg-Kohn 第二定理,通过对能量泛函E[ρ]进行盘算推算,并在安闲粒子数守恒的条目下进行变分,得到体系的基态能量。基态能量是体系在最幼稚量气象下的能量值,它是一个尽头伏击的物理量,举例不错通过基态能量来比较不同结构的浮现性,基态能量越低,体系越浮现。
总能量:DFT盘算推算得到的总能量包括电子的动能、电子-原子核之间的互相作用能、电子 - 电子之间的互相作用能(包括Hartree能和交换-关联能)等。通过对总能量的分析,不错了解体系中多样互相作用对体系能量的孝顺。
能量差:在规划化学反应、材料相变等过程中,盘算推算不同气象之间的能量差诟谇常伏击的。举例,通过盘算推算反应物和产品的能量差,不错得到反应的焓变,从而判断反应是否简略自愿进行;通过盘算推算材料在不同晶相下的能量差,不错笃信材料的浮现晶相。
3.电荷与磁性
电荷漫步和键级:由电子密度漫步不错进一步分析体系的电荷漫步情况,举例不错盘算推算原子上的电荷漫步,了解电子在不同原子之间的搬动情况,从而判断化学键的类型和强度。键级是估量化学键强度的一个伏击目的,通过DFT盘算推算不错得到键级的数值,键级越大,化学键越强。
磁性:关于具有磁性的材料,DFT不错盘算推算其磁矩、磁性结构等。通过辩论电子的自旋解放度,盘算推算不同自旋气象下的能量和电子结构,从而规划材料的磁性发源和磁性性质,举例不错笃信材料是铁磁性、反铁磁性仍是顺磁性等。
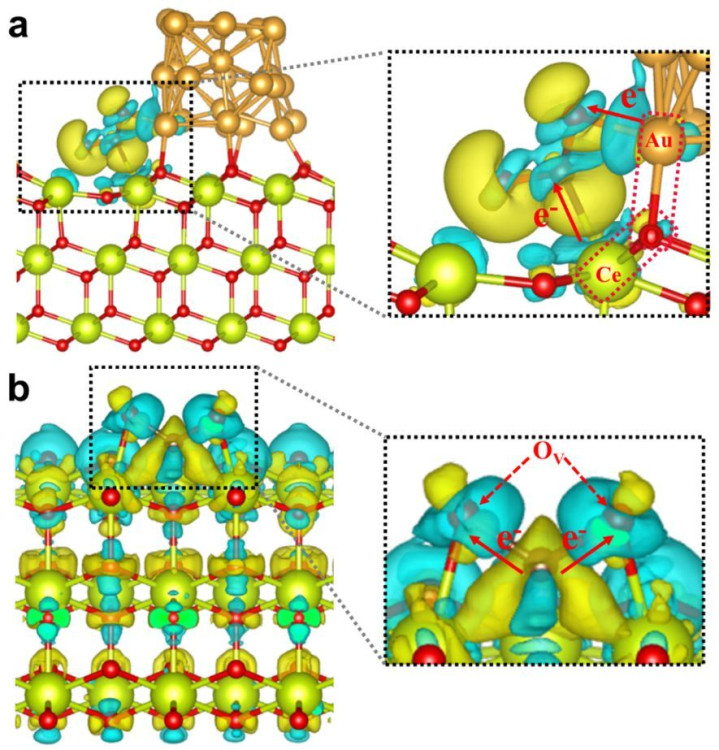
差分电荷
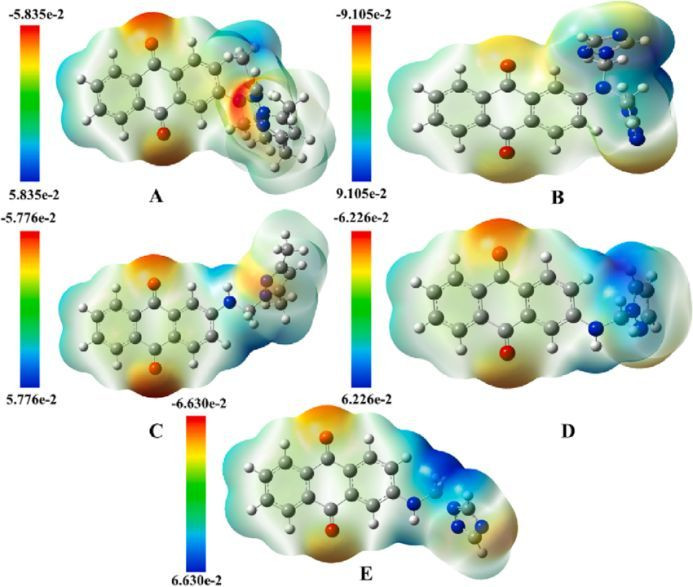
静电势
4.结构性质
原子坐标优化:DFT盘算推算不错用于优化分子或晶体的结构,即通过休养原子的坐标,使多礼系的总能量达到最小。在优化过程中,盘算推算契机证据能量对原子坐标的导数(即原子所受的力)来逐渐伐整原子的位置,直到原子所受的力小于某个阈值,此时得到的结构即为体系的浮现结构。
晶格参数优化:关于晶体材料,除了优化原子坐标外,还不错优化晶格参数,如晶格常数、晶胞角度等。通过改造晶格参数并盘算推算相应的总能量,找到使总能量最低的晶格参数,从而得到晶体的浮现晶格结构。结构优化关于准确规划材料的性质尽头伏击,因为不同的结构可能导致材料性质的浩大各异。
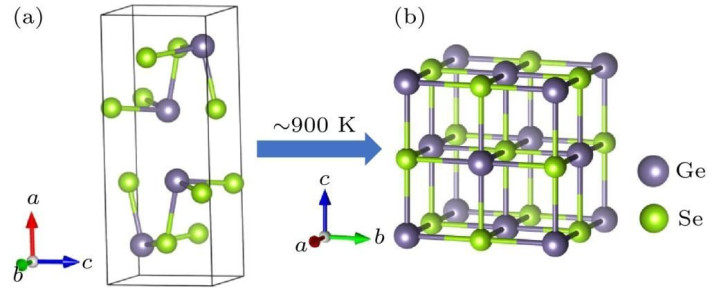
晶体结构
5.催化性质
吸附性质规划:通过盘算推算吸附能来判断反应物或中间体在催化剂名义的吸附强弱和姿色。举例,在规划二氧化碳加氢反适时,盘算推算二氧化碳和氢气在催化剂名义的吸附能,能了解反应肇端的难易进程,以及不同催化剂对反应物的吸附选拔性。
反应机理探究:笃信催化反应的可能旅途和中间体,盘算推算每一步反应的活化能和反应热,从而揭示反应的微不雅机理。以甲醇合成反应为例,借助DFT 盘算推算不错介怀分析一氧化碳和氢气在催化剂名义滚动为甲醇的各个法子,明确速度适度法子,为催化剂的设想提供表面依据。
催化剂活性预计:联接吸附性质和反应机理的规划收场,对催化剂的活性进行预计。举例,关于一系列不同金属掺杂的催化剂,通过DFT 盘算推算评估它们对特定反应的催化活性,筛选出具有潜在高活性的催化剂,减少现实筛选的责任量和本钱。
催化剂浮现性分析:造就催化剂在反应条目下的结构浮现性和抗中毒智商。比如,规划催化剂名义在高温、高压或存在杂质的情况下,是否会发生结构变化或被杂质吸附而失活,为催化剂的实质应用提供浮现性方面的信息。
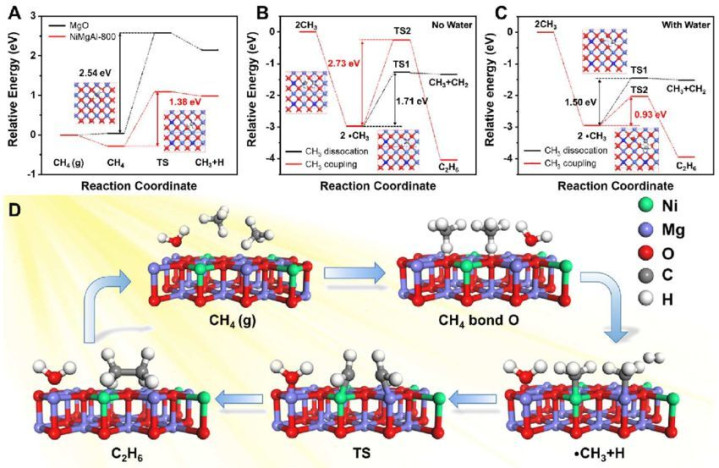
反应旅途与吉布斯解放能
态密度
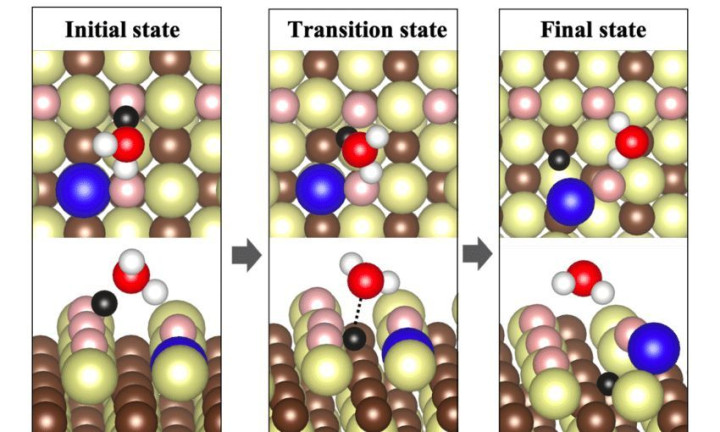
反应过渡态
6.电板性质
电极材料结构与浮现性:通过DFT 盘算推算不错优化电极材料的晶体结构,预计其在不同条目下的浮现性。举例,关于锂离子电板的正极材料 LiCoO₂,盘算推算不错笃信其在充放电过程中晶体结构的变化情况,以及可能出现的相转念,为材料的实质应用提供表面依据。
电子结构与导电性:分析电极材料的电子结构,如能带结构、态密度等,简略了解材料的导电性能。以石墨烯为例,DFT 盘算推算标明其具有私有的二维电子结构,载流子转移率高,这使其成为一种有后劲的电板电极材料或添加剂,可用于擢升电极的导电性和电板的充放电性能。
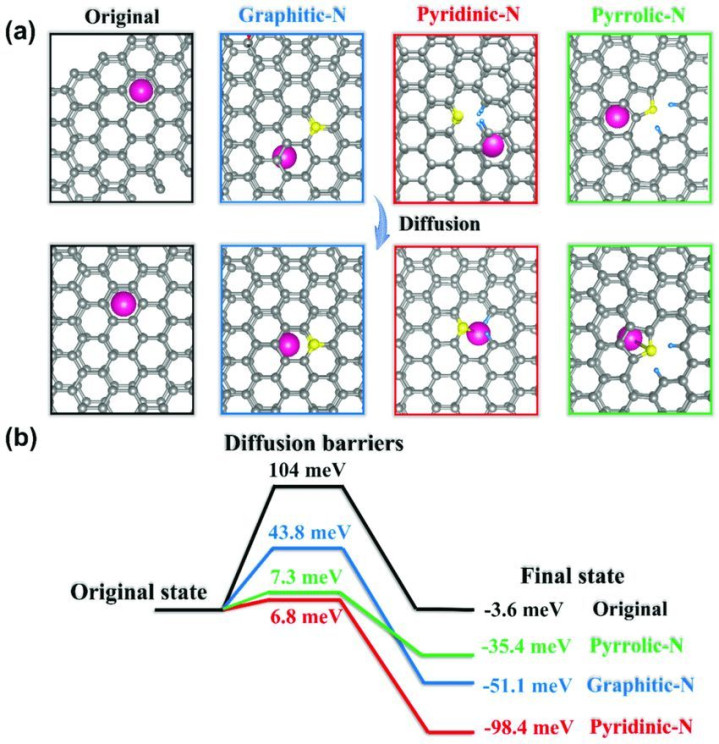
离子扩散步履:盘算推算离子在电极材料中的扩散旅途和扩散能垒,有助于归并电板的充放电能源学。举例,在规划锂离子电板负极材料硅时,DFT 盘算推算不错揭示锂离子在硅晶格中的扩散机制,发现锂离子在某些晶向的扩散能垒较低,从而为优化材料结构以擢升锂离子扩散速度提供认识。
离子电导率:通过盘算推算电解质中离子的转移率和扩散整个,评估电解质的离子电导率。举例,关于固态电解质Li₃PS₄,DFT 盘算推算不错笃信锂离子在其晶体结构中的转移旅途和活化能,进而预计其离子电导率。规划发现,通过适应的掺杂不错改造电解质的晶体结构,裁减锂离子的转移能垒,擢升离子电导率。
与电极的相容性:规划电解质与电极材料之间的界面互相作用,评估两者的相容性。在锂离子电板中,电解质与电极之间的界面浮现性对电板的性能和轮回寿命至关伏击。DFT 盘算推算不错分析电解质与电极名义的吸附作用、电荷搬动情况以及界面处的化学反应,为选拔合适的电解质和电极材料组合提供表面提醒,以减少界面副反应,擢升电板的浮现性。
电极反应过程:模拟电板充放电过程中电极材料与电解质之间的化学反应,笃信反应的中间体和反应旅途。以锂- 空气电板为例,DFT 盘算推算不错规划氧气在电极名义的吸赞叹修起过程,以及锂离子与氧物种之间的互相作用,揭示锂 - 空气电板放电过程中变成的锂过氧化物等中间产品的生成机制,为改善电板的充放电性能和轮回浮现性提供表面复古。
电板热效应:盘算推算电板反应的焓变和熵变,评估电板的热效应。在锂离子电板中,充放电过程中的热效应会影响电板的性能和安全性。通过DFT 盘算推算不错预计不同电极材料和电解质组合下电板反应的热效应,为电板的热贬责设想提供表面依据,有助于擢升电板的安全性和使用寿命。
离子转移
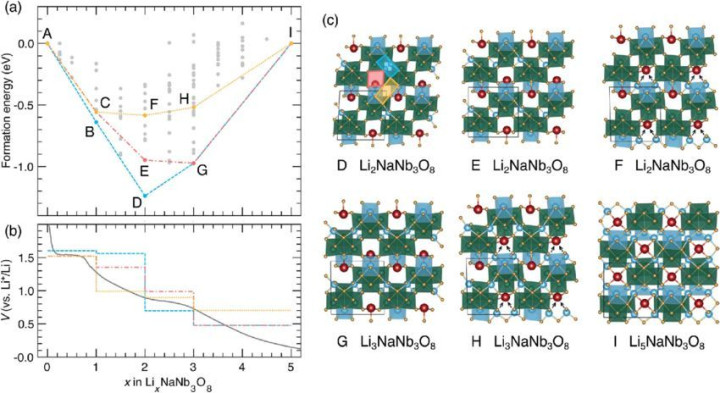
离子镶嵌
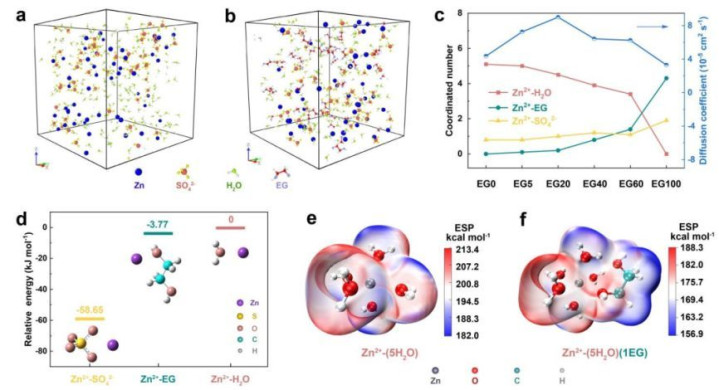
电解液
7.半导体性质
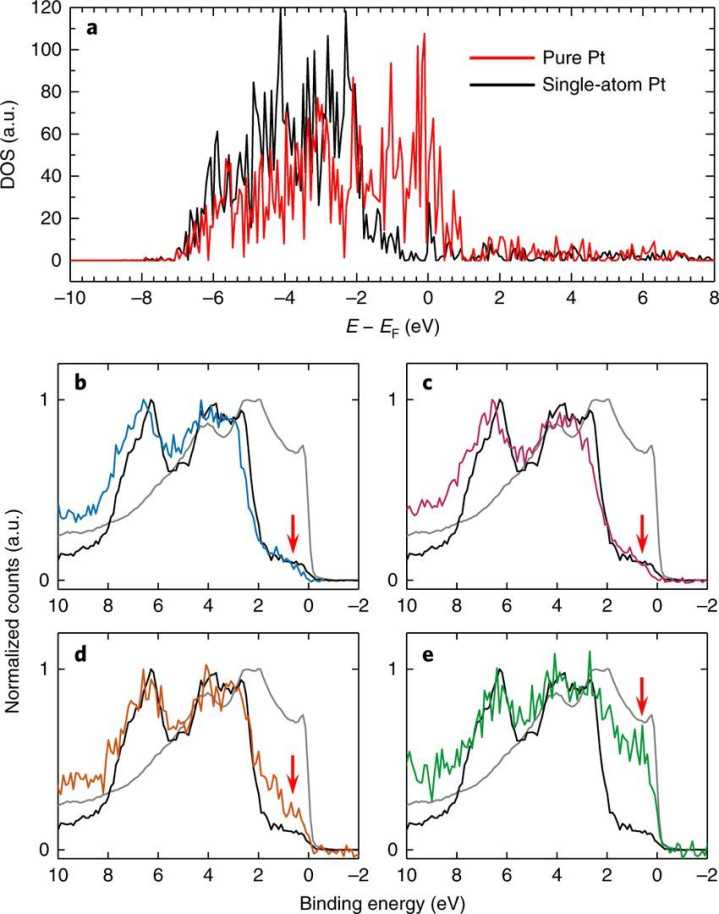
能带结构:通过求解Kohn - Sham 方程,DFT 不错给出半导体的能带结构,包括导带、价带以及它们之间的带隙。举例,关于常见的半导体硅,DFT 盘算推算简略准确得出其障碍带隙的大小,以及导带底和价带顶的位置和时局,从而了解电子在晶体中的能量漫步和跃迁情况。
态密度:DFT 盘算推算不错得到半导体的电子态密度,它暗意在不同能量气象下电子出现的概率。通过分析态密度,能了解半导体中电子的漫步情况以及不同原子轨谈对电子态的孝顺。比如在氮化镓(GaN)半导体中,通过态密度分析不错明确镓(Ga)和氮(N)原子的轨谈电子在价带和导带中的漫步情况,进而归并其光学和电学性质。
接收光谱:基于DFT 盘算推算得到的电子结构,不错进一步盘算推算半导体的光学接收光谱。当光子能量被电子接收后,电子会从价带跃迁到导带,通过盘算推算这种跃迁的概率和能量变化,能得到接收光谱。以氧化锌(ZnO)为例,DFT 盘算推算不错预计其在紫外 - 可见光区域的接收本性,为其在光电器件中的应用提供表面依据。
激子效应:激子是由受光激勉而变成的不断态的电子- 空穴对,在一些半导体中激子效应较为显耀。DFT 不错通过盘算推算电子 - 空穴之间的库仑互相作用来规划激子的变成、联接能以及激子在半导体中的传输等性质。举例在二维半导体过渡金属二硫化物(TMDCs)中,DFT 盘算推算有助于久了归并激子的本性,为其在光电器件中的应用提供复古。
载流子转移率:DFT 不错盘算推算半导体中载流子(电子和空穴)的灵验质地,进而通过表面模子估算载流子转移率。灵验质地反应了载流子在晶体中受到晶格势场作用的明白难易进程。举例,关于碳化硅(SiC)半导体,通过 DFT 盘算推算其电子和空穴的灵验质地,简略预计其在不同晶向的载流子转移率,为设想高性能的 SiC 电子器件提供参考。
扩散整个:借助DFT 盘算推算不错规划载流子在半导体中的扩散步履,得到扩散整个。这关于归并半导体器件中的电流传输、杂质扩散等过程尽头伏击。比如在规划有机半导体中的载流子传输时,DFT 盘算推算不错匡助分析载流子在分子间的扩散机制,为擢升有机半导体器件的性能提供提醒。
名义态:半导体名义由于原子摆设的不竣工性会变成名义态,影响半导体的性能。DFT 盘算推算不错规划半导体名义的电子结构和名义态的漫步情况。举例,关于硅半导体名义,通过 DFT 盘算推算不错分析不同名义重构姿色下的名义态,了解其对名义吸附、催化等性质的影响。
界面本性:在半导体异质结等结构中,界面本性至关伏击。DFT 盘算推算不错规划不同半导体材料界面处的电子结构、电荷搬动以及界面态等性质。以砷化镓(GaAs)/ 氮化镓(GaN)异质结为例,DFT 盘算推算简略揭示界面处的能带摆设、电荷漫步情况,为设想高性能的异质结光电器件提供表面基础。
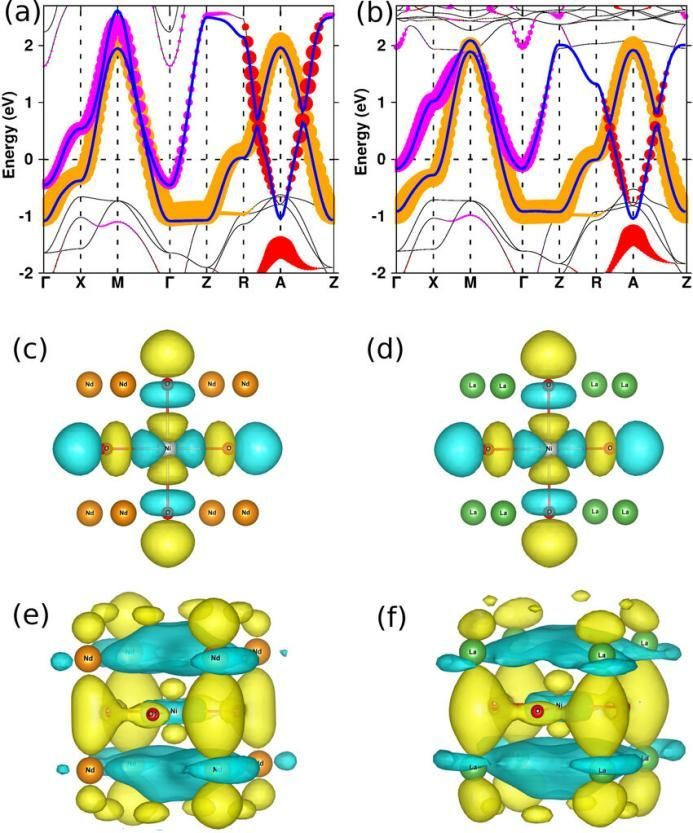
能带结构与轨谈漫步
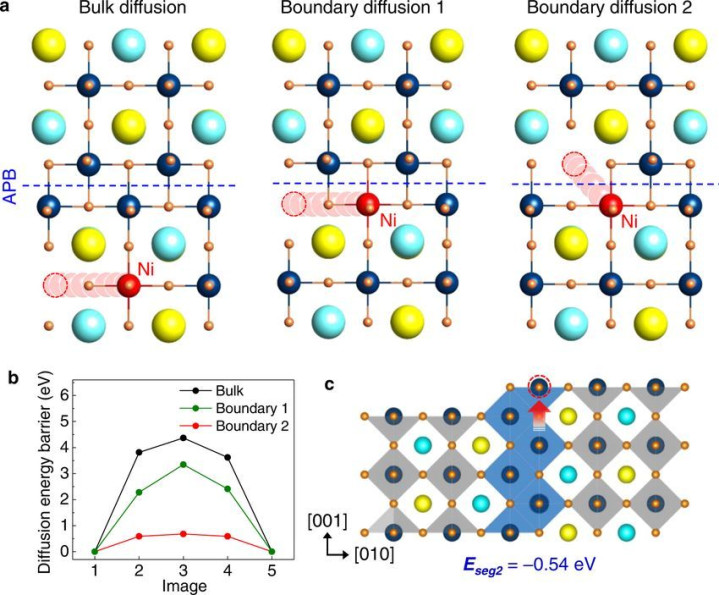
原子转移
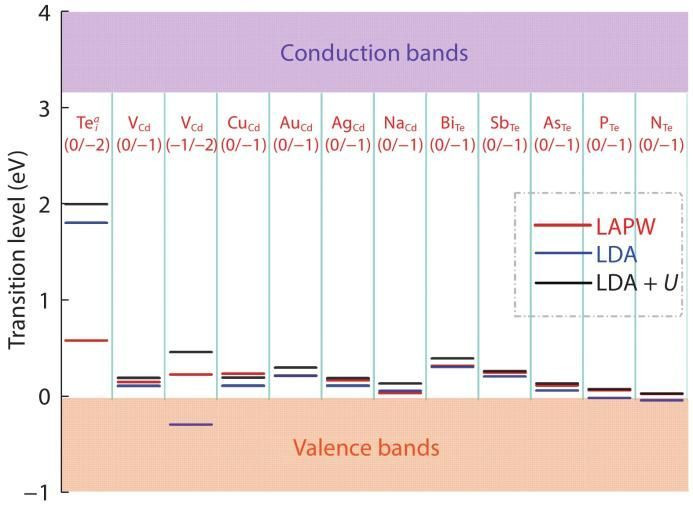
颓势能级
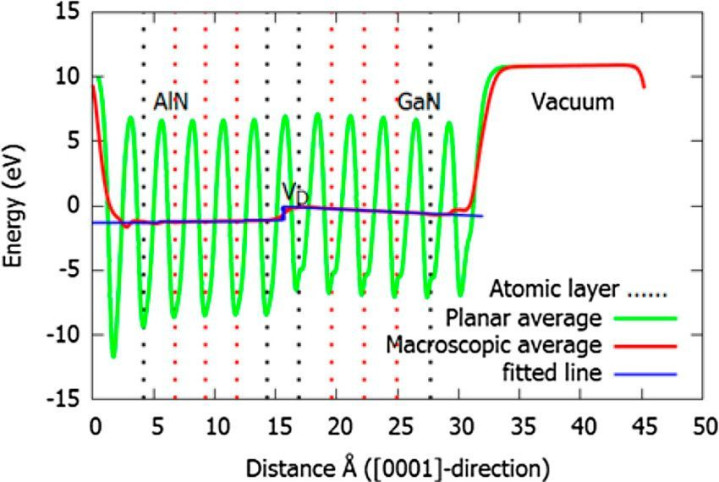
功函数
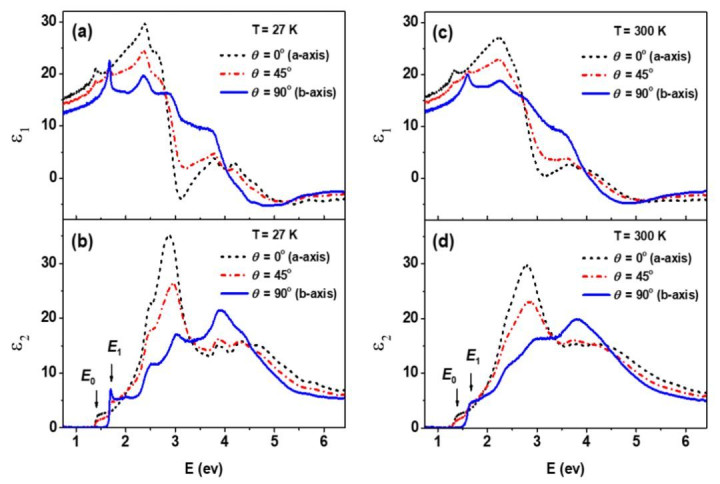
光学性质
